Visit our counting principle post to learn more
Definition
n!=1×2×3.....×n
Fact 0!=1
We will soon discuss the reason behind it.
NOTE
2n!=2ⁿn![1*3*5....(2n-1)]
Illustrations
Do it yourself:
Illustration 1
Find the value of 5!
Answer:- 120
Solution
5!=1×2×3×4×5=120
Illustration 2
n is a number less than 14 how many values can n take if n+1 is a factor of n!
Answer-5
Solution
First let us use trial or error.
For 2!, 3 is not a factor.
For 3!, 4 is not a factor.
For 4!, 5 is not a factor.
........................................................
Now a prime number has only two factors 1 and itself.
So n+1 cannot be prime
Prime numbers smaller than or equal to 14 are 13,11,7,5,2
So n cannot be 12 ,10, 6, 4, 1.
Now let us think from 7.
If n is 7
7! has a factor 8
Since 7!=1×2×3×4×5×6×7=1×3×5×6×7×2 ×4=1×3×5×6×7×8
9 is not a factor of 8!
10 is a factor of 9!
12 is a factor of 11!
14 is a factor of 13!
So we have 5 possible cases.
Illustration 3
Find the maximum value of a, such that 2ᵃ divides 100!
Solution
[100/2]+[100/2²]+[100/2³]+[100/2⁴]+[100/2⁵]+[100/2⁶]+[100/2⁷]........
Important note- this method is valid for prime numbers like 2,5,7,11,......
[*] Denotes greatest integer function
=97
Similar questions
1) Find the maximum value of n such that 5ⁿ is a factor of 100!.
Answer-24
Illustration 4
Find the number of consecutive zeros at the end of 100!
Or
Find the maximum value of n such that 10ⁿ is a factor of 100!
Answer-24
Solution
Number of zeros can be find out by 2ˣ × 5ˣ= 10ˣ
From our earlier observation we have the highest power of 2 and 5
2⁹⁷ × 5²⁴=2⁷³×(2²⁴×5²⁴)=2⁷³×10²⁴
So there are 24 zeros
Incorrect solution
[100/10]+[100/10²]+[100/10³]+...=11
But the above solution is incorrect.
Since it is valid for only prime number
Problems
Find the value of n
Answer-8
2) let the value of the below given expression is k where k is an integer
Find the largest possible value of n
Answer-28
Solution
5!= 120 = 5×4×3×2×1 = 5×2³x3
The above expression is equal to
120!/120ⁿ
We can find the factors which comes as 120²⁸
3)Find the value of
Answer-1
4) Find the unit digit of
(1!)³+(2!)³+(3!)³....+(2020!)³
Answer-9
Solution
From 5! Onwards we have unit digit as 0
5!=1×2×3×4×5=1×3×4×(2×5)=1×3 ×4×10
6!=6×5!
7!=7×6×5!
n!=k×5! (If n>5)
So unit digit of cube of
5! is 0
6! is 0
7! is 0
8! is 0
.......
(1!)³=1
(2!)³=2³=8
(3!)³=6³ unit digit is 6
(4!)³=24³ unit digit is 4
So unit digit of the expression
1+8+6+4=19
Is 9
Q)Show that (kn)! is divisible by (n!)ᵏ
Click on subscribe button above to get the latest update on time
Visit our counting principle post to learn more



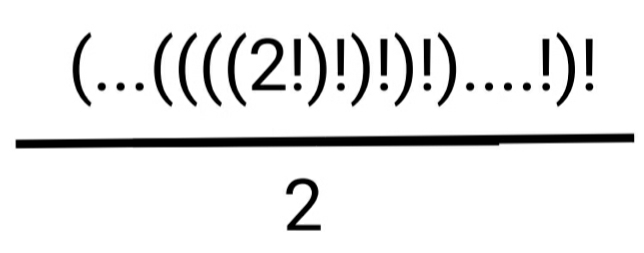
No comments:
Post a Comment
For any queries drop a mail at: teammathfreaks@gmail.com